Machine Learning con Scikit-Learn

Machine Learning con Scikit-Learn

Aprendizaje Automático con scikit-learn

Scikit-learn es una librería enorme con docenas de algoritmos de Machine Learning. Afortunadamente, el proceso para ejecutarlos sobre un conjunto de datos es muy general

Simplificando masivamente, se suelen seguir estos pasos:

1. Preparación: Importamos los módulos necesarios y leemos los datos
2. Selección de características: Elegimos las características más importantes de nuestros datos, scikit-learn facilita algoritmos como PCA para esto.
3. Train-test split (aprendizaje supervisado): Dividimos los datos en conjuntos de entrenamiento y prueba (y también validación)
4. Entrenamiento: Llamamos al método .fit() de nuestro Estimator (Estimator $\approx$ Algoritmo de Machine Learning)
5. Predición: Llamamos al método .predict() del Estimator para realizar las predicciones
6. Evaluación y selección de hiper-parámetros: A partir del error obtenido, podemos decidir si el modelo es suficientemente bueno o debemos cambiar los parámetros o el algoritmo (en aprendizaje supervisado, midiendo el error con los datos de prueba, en aprendizaje no supervisado, usando otra métrica)
7. Representación de resultados: Usando matplotlib o seaborn, podemos visualizar las predicciones.

Selección de algoritmos

Saber qué algoritmo escoger en cada paso es complicado, y se escapa de los objetivos de este curso$\dots$

En esta clase, veremos algunos ejemplos básicos de regresión (regresión lineal) y clustering (K-Means).

Regresión lineal

Buscamos encontrar la relación entre la variable objetivo o dependiente y una o más variables explicativas o independientes

Veremos el método más sencillo, regresión lineal con least-squares (que probablemente recordéis de los cursos de estadística). Scikit-Learn ofrece una implementación en la clase LinearRegression().

Notebook - Regresión linear con Scikit-Learn

Dataset de datos de estudiantes

Clustering con k-means

Ahora nos enfrentaremos a otro problema, el clustering o agrupación de datos. Este problema es de aprendizaje no supervisado, ya que no tenemos ninguna variable objetivo. Entre los algoritmos de clustering, K-Means es el más conocido.

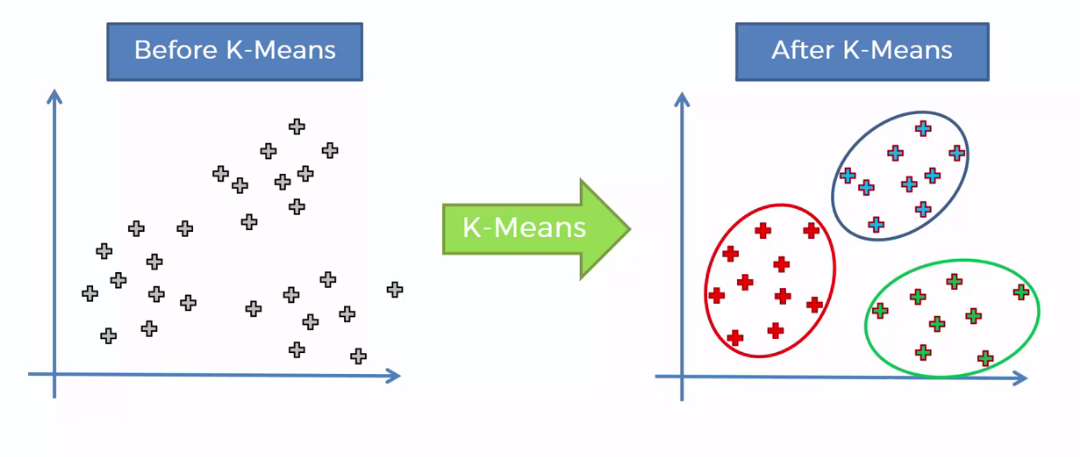
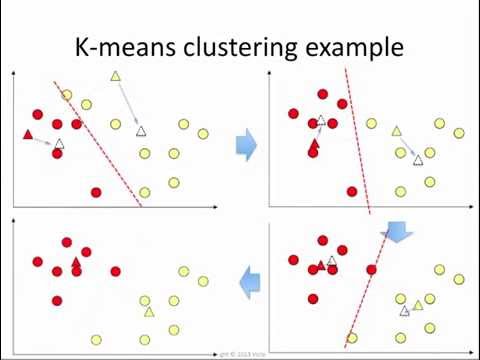
K-Means es un algoritmo iterativo que clasifica los datos a partir de su distancia a un conjunto de centroides. El algoritmo es el siguiente:

1. Inicio: se asignan $n$ centroides aleatoriamente sobre el espacio.
2. Asignación: a cada punto le asignamos su centroide más cercano (por ejemplo, usando la distancia euclídea). Formamos así $n$ grupos separados.
3. Recálculo de centroides: si no hemos llegado a cierta tolerancia o número máximo de iteraciones en el error, recalculamos los centroides a partir de la media de los puntos en cada grupo.

Más sobre clustering

Formalmente, dado un conjunto $(x_1, x_2, \dots, x_n) \subset \mathbb{R}^d$ y un $k \in \mathbb{N}, k \leq n$, en el problema de clustering queremos encontrar una familia de conjuntos $S = \{S_1, S_2, \dots, S_k\}$ tales que todo $x_i$ está en algún $S_j$ y se minimiza la suma de los cuadrados dentro de cada grupo (WCSS): $$ \argmin_S \sum_{i=1}^k \sum_{x_j \in S_i} \left\lVert x_j - \mu_i \right\rVert,$$ donde $\mu_i$ es el centroide de $S_i$, $$ \mu_i = \frac{1}{|S_i|} \sum_{x \in S_i} x.$$

K-Means es un algoritmo que aproxima este problema

Clustering con k-means

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs

# Generamos 1000 puntos aleatorios en 3 clusters, vamos a ver si podemos recuperarlos
X, y = make_blobs(n_samples=1000, centers=3, random_state=42, cluster_std=1.0)

# En primer lugar, escalamos los datos
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Y ahora hacemos K-means especificando el número de clusters a 3
# K-Means usa un estado aleatorio, que debemos prefijar (es como prefijar una semilla)
# NOTA: existen métodos (Elbow method, Silhouette score...) para hallar el número de clusters
# óptimo automáticamente
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X_scaled)

# Extraemos los centros de los clusters y los labels, que nos dicen en qué cluster cae cada punto
centros = kmeans.cluster_centers_
labels = kmeans.labels_

# Plotteamos los puntos con colores de los labels y marcamos los centros de cada cluster
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centros[:, 0], centros[:, 1], c='red', s=100, marker='X')
plt.show()

							

Proyecto final

Encuesta de satisfacción