Introducción a NumPy
Introducción a NumPy
- NumPy (Numerical Python) es uno de los paquetes más importantes para la computación numérica.
- La mayoría de librerías científicas utilizan sus objetos como lingua franca para el intercambio de datos.
- Algunas de sus principales características son:
- ndarray: un array multidimensional que permite realizar operaciones aritméticas y de broadcasting de forma eficiente
- Operaciones vectorizadas
- Funcionalidades para el álgebra lineal, la generación de números (pseudo)aleatorios, transformadas de Fourier, etc.
Pocas veces es necesario usar NumPy directamente; veremos solo las características más importantes que ofrece.
- Documentación completa aquí
- La página oficial también incluye muchos tutoriales de alta calidad (en inglés):
- Absolute basics for beginners
- NumPy fundamentals
- NumPy how-tos
- NumPy tutorials (más basados en proyectos)
(Las imágenes usadas en estas diapositivas están principalmente sacadas de estos tutoriales)
Qué es numpy?

Ya hemos hablado de las listas lista = [1, "python", [1,3]], que son colecciones lineales de elementos
También podemos crear matrices como listas anidadas:
M =
[[0,1], [1,0]] $\;\Longleftrightarrow \; M = \begin{pmatrix}0 \;1 \\ 1 \;0 \end{pmatrix}$
Las listas son muy flexibles al admitir formas irregulares y tipos de datos heterogéneos, pero esta flexibilidad tiene un gran coste en eficiencia.
Para remediar estos problemas, NumPy nos da una estructura de datos llamada array n-dimensional (ndarray)
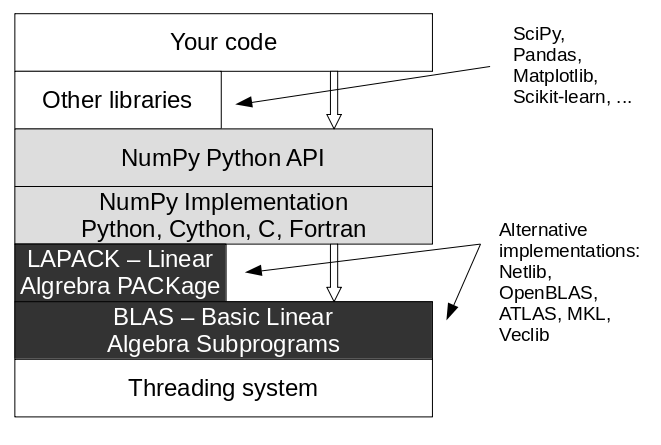
ndarrays
- Tienen un tamaño fijo, que se indica en su creación
- Todos sus elementos deben ser del mismo tipo (normalmente numéricos)
- Se pueden indexar de muchas formas, y NumPy provee cientos de operaciones vectorizadas sobre ellos
- Son similares a los vectores de R y de MATLAB, aunque hay ciertas diferencias
import numpy as np
a = np.arange(16).reshape(4,4)
print(a) # array([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11],
# [12, 13, 14, 15]])
print(a.ndim) # 2
print(a.shape) # (4, 4)
print(a.size) # 16
print(a.dtype) # int64
Número de dimensiones
Número de elementos en cada dimensión (tupla)
Número total de elementos
El tipo de dato de los elementos
Atributos fundamentales: ejemplos
ndarray.ndim
data1 = [1., 0.3, 2, 4, -2]
arr1 = np.array(data1)
data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr2 = np.array(data2)
print(arr1.ndim) # 1
print(arr2.ndim) # 2
print(arr1.shape) # (5,)
print(arr2.shape) # (2, 4)
print(arr1.size) # 5
print(arr2.size) # 8
print(arr1.dtype) # float64
print(arr2.dtype) # int32
Resumen de tipos de datos en NumPy
| dtype | Variantes | Descripción |
|---|---|---|
| int | int8, int16, int32, int64 | Enteros con signo |
| - | uint8, uint16, uint32, uint64 | Enteros sin signo (i.e., no negativos) |
| bool | - | Booleanos (True/False) |
| float | float16, float32, float64, float128 | Números de punto flotante. |
| complex | complex64, complex128, complex256 | Números complejos en punto flotante. |
| string_ | - | Cadenas de caracteres de hasta 1 byte |
| object | - | Cualquier objeto de Python |
ndarray: orden de los ejes
Al haber varias dimensiones, tenemos que tener en cuenta el orden de acceso e impresión de elementos. Para arrays en 2 dimensiones, el primer eje axis = 0 son las filas, y el segundo axis = 1 las columnas
a = np.array([[2., 3., 5.],
[7., 8., 9.]])
# El primer eje es de tamaño 2 y el segundo de tamaño 3:
print(np.shape(a)) # (2, 3)
Para $n > 2$, ya no se pueden visualizar los ndarrays como matrices, pero podemos seguir consultando el tamaño de cada eje con np.shape.
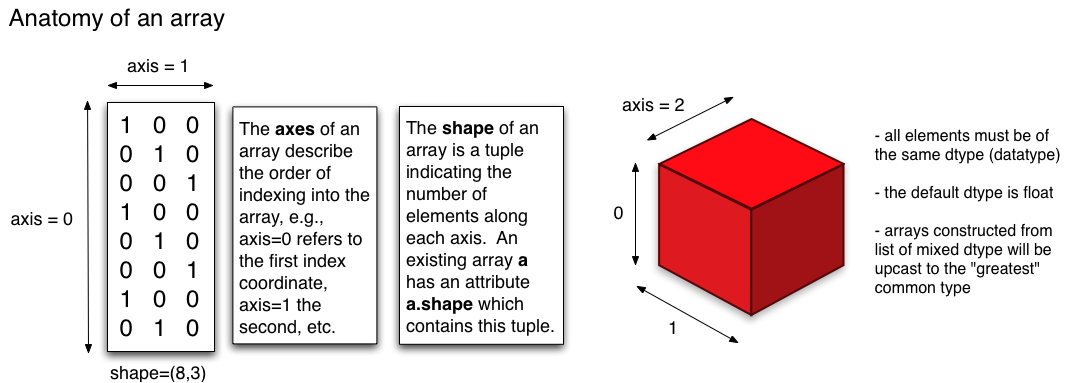
Creación de arrays
Hay muchos mecanismos de creación de arrays n-dimensionales
A partir de otras estructuras (listas y tuplas)
import numpy as np
mi_lista = [1, 2, 3]
# Se puede especificar el tipo de dato
a = np.array(mi_lista, dtype=np.string_)
# y cambiarlo
b = a.astype(float) # array([1., 2., 3.])
# Shape (2, 2, 2), dtype 'int32'
a3D = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
Creación de arrays
Hay muchos mecanismos de creación de arrays n-dimensionales
Utilizando np.arrange y np.linspace para crear listas de rangos separados
import numpy as np
# Crear un array de 0 a 10, con salto de 2
a = np.arange(0, 10, 2) # array([0, 2, 4, 6, 8])
# Crear un array de 0 a pi, con 10000 elementos
b = np.linspace(0, np.pi, 10000) # array([0.00000000e+00, 3.14190684e-04, 6.28381369e-04, ...,
# 3.14096427e+00, 3.14127846e+00, 3.14159265e+00])
Creación de arrays
Hay muchos mecanismos de creación de arrays n-dimensionales
Mediante funciones de creación:
import numpy as np
# Matriz 3x3 con 0 en todas las posiciones
zeros = np.zeros((3, 3))
# Matriz 2x4 con 1 en todas las posiciones
ones = np.ones((2, 4))
# Matrix 2x2 con valor infinito en todas las posiciones
mat_inf = np.full((2, 2), np.inf)
# Matriz identidad de 4x4
id = np.eye(4)
# Matriz 2x3 con valores aleatorios en [0,1)
rand_arr = np.random.rand(2, 3)
Creación de arrays
Hay muchos mecanismos de creación de arrays n-dimensionales
import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
# Usando vstack (equivalente a np.concatenate con axis=0)
vstacked = np.vstack((a, b)) # array([[1, 2],
# [3, 4],
# [5, 6],
# [7, 8]])
# Usando hstack (equivalente a np.concatenate con axis=1)
hstacked = np.hstack((a, b)) # array([[1, 2, 5, 6],
# [3, 4, 7, 8]])
Ya hemos visto varias formas de crear arrays, pero también es importante saber que (casi) todas las operaciones que explicaremos más adelante también crean arrays nuevos.
Hay alguna otra forma más de crear arrays, por ejemplo a partir de ficheros. En la siguiente clase leeremos ficheros con Pandas, así que nos saltamos esto de momento, consultar: Array Creation guideIndexación y slicing
En un array de NumPy, el indexado es parecido al de una lista normal de Python, pero en varias dimensiones
a = np.array([[1, 2], [3, 4], [5, 6]])
# Elementos específicos
print(a[0, 0]) # 1
print(a[1, 2]) # 4
# Segunda fila
print(a[1]) # [3, 4]
# Segunda columna
print(a[:, 1]) # [2, 4, 6]
# Slicing en varias dimensiones
# : indica todos los elementos en el respectivo eje
print(a[1:, 1:]) # [[4]
# [6]]

Indexación y slicing
También podemos indexar a partir de otros arrays
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Filas 2 y 1
b = np.array([1, 0])
print(a[b]) # array([[4, 5, 6],
# [1, 2, 3]])
# Todas las filas, y luego columnas 1 y 2
c = np.array([1,2])
print(a[:, c]) # array([[2, 3],
# [5, 6],
# [8, 9]])
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(a[a > 5]) # array([6, 7, 8, 9])
Reshaping
Con arr.reshape() podemos cambiar la forma de un array
Por ejemplo podemos pasar de un array $6 \times 2$ a uno $3 \times 4$:
import numpy as np
a = np.arange(12).reshape(6, 2)
print(a.shape) # (6, 2)
b = a.reshape(3, 4)
print(b.shape) # (3, 4)
Pro tip: Si no sabemos el tamaño de una de las dimensiones, podemos hacer que NumPy la calcule inmediatamente poniendo $-1$ en ella.
import numpy as np
a = np.arrange(15000)
b = a.reshape(-1, 3, 1000)
print(b.shape) # (5, 3, 1000)
Reshaping
Con np.ravel podemos linealizar un array y con arr.T hallar la traspuesta de una matriz!
import numpy as np
a = np.array([[1, 2], [3, 4]])
print(a.ravel()) # array([1, 2, 3, 4])
print(a.T) # array([[1, 3],
# [2, 4]])
También podemos añadir nuevos ejes con np.newaxis o np.expand_dims
import numpy as np
a = np.array([1, 2, 3])
print(a[:, np.newaxis]) # array([[1],
# [2],
# [3]])
Operaciones sobre arrays
- Las operaciones sobre arrays de NumPy son vectorizadas, es decir, se ejecutan sobre todo el array sin necesidad de usar bucles explícitos en Python.
- Esto no solo hace más conciso el código, sino que reduce el tiempo de ejecución gracias a la implementación interna de NumPy (ya que los procesadores modernos pueden ejecutar muchas operaciones a la vez)
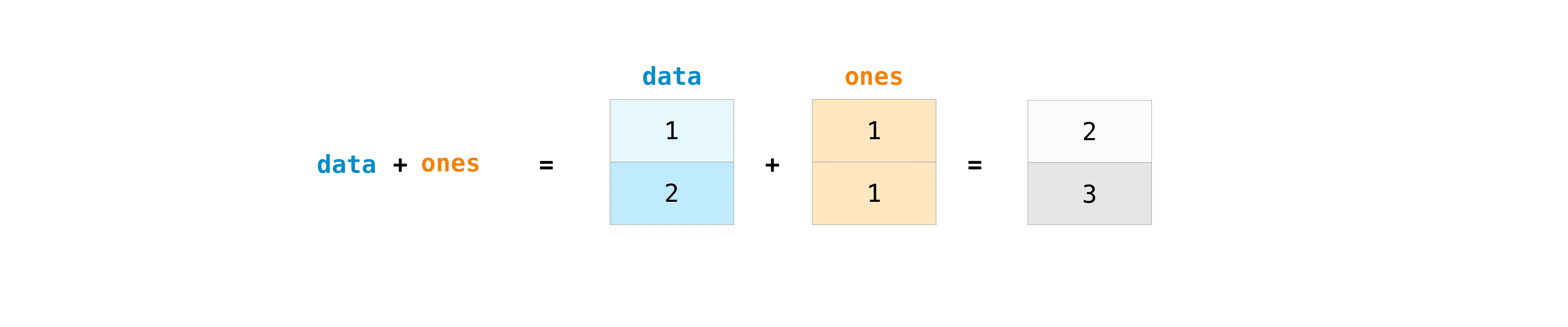
De esta forma, podemos aplicar operaciones básicas simplemente como:
import numpy as np
data = np.array([1, 2])
ones = np.ones(2, dtype=int)
# Operaciones aritméticas vectorizadas
print(data + ones) # array([2, 3])
print(data - ones) # array([0, 1])
print(data * data) # array([1, 4])
print(data / data) # array([1, 1])
# NO HACER ESTO
for i in range(len(data)):
data[i] += 1
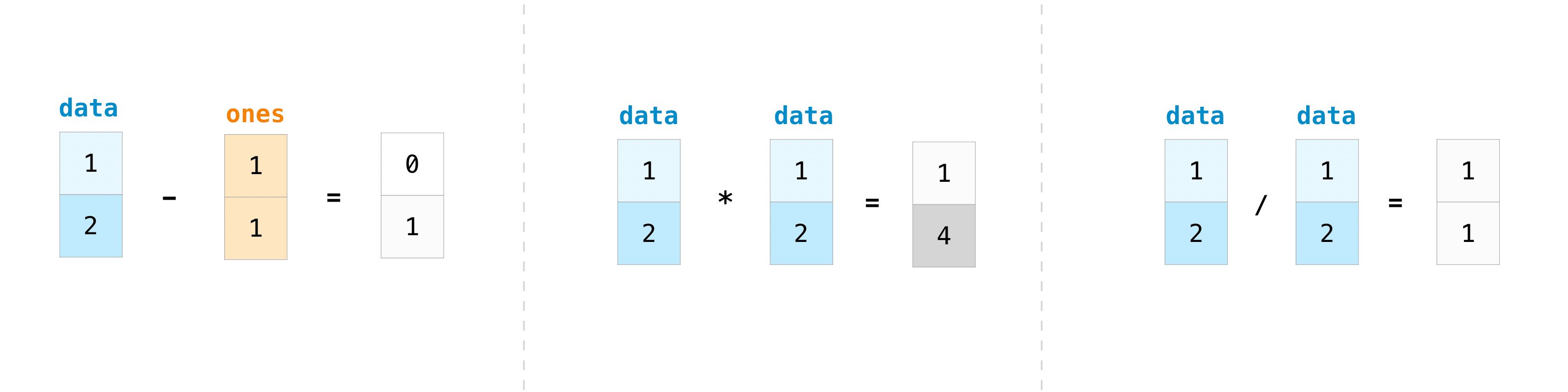
Operaciones sobre arrays
Además de operar sobre 2 arrays, podemos agregar los elementos de uno mediante operadores como la suma, el máximo o el mínimo, entre muchos otros.
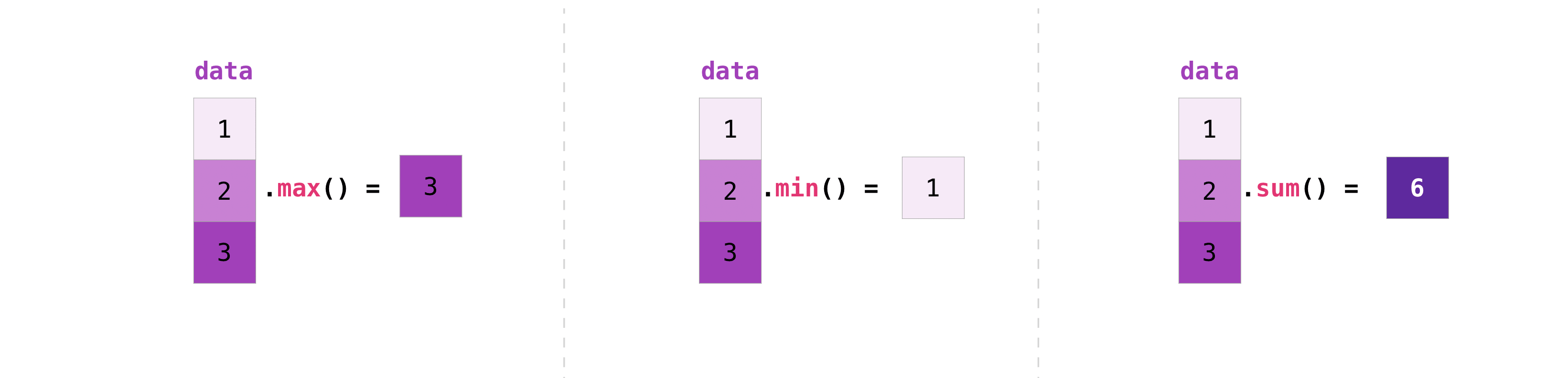
En vez de ejecutar esto sobre todo un array, podemos reducir en cada eje
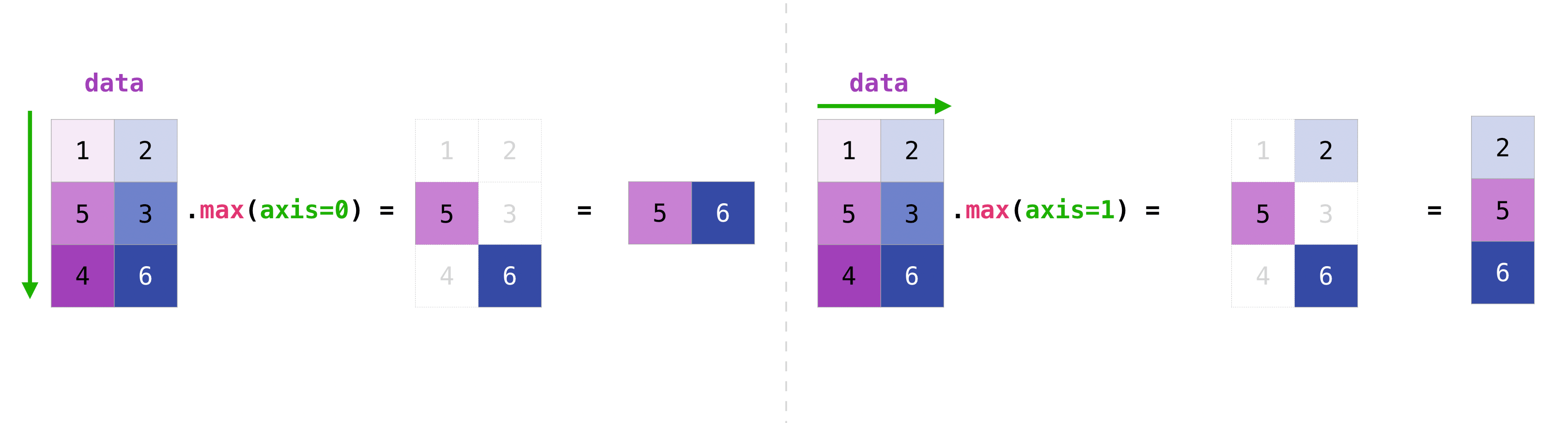
import numpy as np
data = np.array([[1, 2], [3, 4]])
print(data.sum()) # 10
print(data.max()) # 4
print(data.sum(axis=0)) # array([4, 6])
print(data.max(axis=1)) # array([2, 4])
También es importante el broadcasting, que permite operar un array grande con otro pequeño (incluso con un escalar) "copiando" el pequeño varias veces a lo largo de un eje.
import numpy as np
a = np.array([1, 1, 1])
print(a + 5) # array([6, 6, 6])
b = np.array([[1, 2, 3], [4, 5, 6]])
print(b + a) # array([[2, 3, 4],
# [5, 6, 7]])
print(1 / (2 * a)) # array([0.5, 0.5, 0.5])
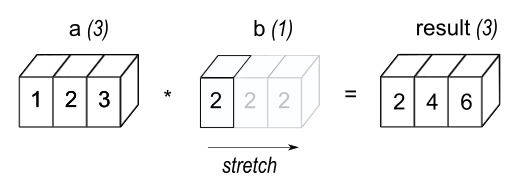
Existen algunas normas sobre cuando podemos hacer esto, se pueden consultar aquí
Operaciones sobre arrays
Algunas otras cosas que podemos hacer sobre arrays:
Comparaciones
(se usa mucho para indexar)
a = np.array([1, 2, 3])
b = np.array([3, 2, 1])
print(a == b) # array([False, True, False])
print(a > b) # array([False, False, True])
Ordenar
(También existe np.argsort para obtener los índices de ordenamiento)
a = np.array([3, 1, 2])
print(np.sort(a)) # array([1, 2, 3])
Funciones universales (es decir, otras funciones matemáticas que ya vienen implementadas)
a = np.array([1, 2, 3])
print(np.exp(a)) # array([ 2.718, 7.389, 20.085])
print(np.sqrt(a)) # array([1.000, 1.414, 1.732])
print(np.mean(a)) # 2.0
Producto de matrices (la función preferida de los que tienen que hacer boletines de álgebra)
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
print(a @ b) # array([[19, 22],
# [43, 50]])
# También se pueden usar np.dot(a, b) o a.dot(b)
Operaciones sobre arrays
Algunas otras cosas que podemos hacer sobre arrays:
Operaciones estadísticas
(sobre todo el array o por filas/columnas)
a = np.array([[1, 2, 3], [4, 5, 6]])
print(np.max(a)) # 6
print(np.argmax(a)) # 5
# np.unravel_index(np.argmax(a), a.shape) --> (1, 2)
print(np.sum(a)) # 21
print(a.mean(axis=1)) # [2., 5.]
print(a.sum(axis=0)) # [5, 7, 9]
print(np.std(a)) # 1.7078...
Operaciones booleanas y expresiones lógicas(muy similares a las de Pandas)
bools = np.array([False, False, True, False])
bools.any() # True
bools.all() # False
# Nota: "and" y "or" no funcionan sobre arrays booleanos
# Hay que usar & y |
nums = np.array([2, 4, 8, 3, 7])
cond = (nums == 2) | (nums >= 7)
# cond: [True, False, True, False, True]
# Versión NumPy de la list comprehension
# [x if cond else y for elem in array]
nums2 = np.where(nums > 4, "si", "no")
# nums2: ['no', 'no', 'si', 'no', 'si']
Operaciones sobre arrays
Además de las operaciones básicas, NumPy nos proporciona cientos de funciones matemáticas que aplicar sobre arrays. Algunas de ellas están en paquetes separados, por ejemplo:
- numpy.linalg. Incluye funciones para álgebra lineal. Incluye resolución de sistemas lineales, cálculo de autovalores, descomposiciones SVD, de Cholesky, etc. (ANM in a box).
- numpy.random. Incluye funciones para crear arrays aleatorios que sigan ciertas distribuciones estadísticas (e.g. binomial, normal, beta, chisquare, gamma) hacer permutaciones, etc.
- numpy.fft. Contiene funciones para calcular transformadas de Fourier en varias dimensiones.
También existe la librería SciPy, que no cubriremos en este curso, pero expande NumPy incorporando muchas más funciones de computación científica.
Vista vs Copia
a.k.a. piedras con las que tropezaréis más de una y más de dos veces
Al copiar un objeto, obtenemos un nuevo objeto idéntico al original, pero independiente. Si hacemos cambios sobre la copia, el original permanece inalterado.
Una vista de un objeto ofrece una nueva representación de sus datos, pero no los copia. Por tanto, si se opera sobre la vista, también cambiará el objeto original.
Algunas operaciones de NumPy, como las operaciones de indexado o reshape(), devuelven vistas. Otras, como astype(), devuelven copias.
arr = np.array([1, 2, 3, 4])
vista = arr.reshape((2, 2))
vista[0, 0] = -1
print(arr[0]) # -1
arr[1:] = 10
print(vista) # [[-1 10]
# [10 10]]
copia = arr.astype(float)
copia[0] = 5.0
print(arr[0]) # -1
En resumen...
- NumPy es una librería fundamental para el cálculo numérico en Python.
- Los ndarrays son más eficientes que las listas de Python.
- Los ndarrays tienen operaciones vectorizadas rápidas, que además simplifican
código
(o lo complican, depende como las uses) - Hay muchas librerías que usan NumPy para implementar todo tipo de estructuras a partir de
ndarray
(por ejemplo Pandas, que veremos en la siguiente clase!)